GPT-1 논문 리뷰를 하던 중 문득 "multi-layer transformer decoder를 사용할 때 input으로 사용할 $h_0$는 어떻게 만들어질까?"라는 궁금증이 들었다.

GPT에서 multi-layer transformer decoder를 사용해서 Maksed self-attention을 하기 전에 token들의 context vector(U)와 token embedding matrix($W_e$)를 곱한 후 positional embedding matrix($W_p$)를 더해서 input으로 사용할 $h_0$를 만든다.
이때 각 matrix들의 차원은 어떤 식으로 구성될까?
이를 알기 위해서는 텐서(Tensor)의 개념을 짚고 넘어가야 한다.
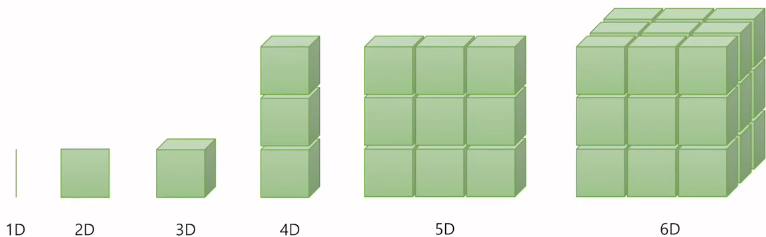
딥 러닝을 하게 되면 다루게 되는 가장 기본적인 단위는 벡터, 행렬, 텐서이다. 차원이 없는 값을 스칼라(위의 그림에는 없음), 1차원으로 구성된 값을 벡터라고 한다.
2차원으로 구성된 값을 행렬(Matrix)라고 하고, 3차원이 되면 텐서(Tensor)라고 부른다.
사실 우리는 3차원의 세상에 살고 있으므로, 4차원 이상부터는 머리로 생각하기는 어렵다.
4차원은 3차원의 텐서를 위로 쌓아 올린 모습으로 상상해 보자. 5차원은 그 4차원을 다시 옆으로 확장한 모습이고, 6차원은 5차원을 뒤로 확장한 모습으로 볼 수 있다. (엄밀한 정의는 아니다. 직관적으로 이렇게 이해해보자 라는 것이다.)
Computer Vision 분야에서의 3차원 텐서와 NLP 분야에서의 3차원 텐서는 조금 다르다.
우리는 현재 NLP에서 사용할 것이므로 NLP에서의 3차원 텐서를 살펴보자.
NLP에서는 보통 (batch size, 문장 길이, 단어 벡터의 차원)이라는 3차원 텐서를 사용한다.
직관적으로 표현하면 다음과 같다.
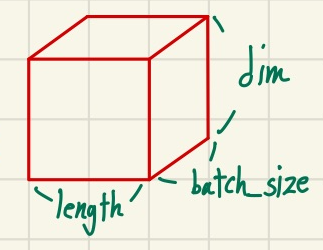
자 이제 3차원 텐서(Tensor)에 대해 이 정도의 개념을 가지고 다시 우리가 알고 싶었던

로 돌아가보자.
쉽게 예제를 통해 이해해보자.
아래와 같이 4개의 문장으로 구성된 전체 훈련 데이터가 있다. (띄어쓰기를 기준으로 토큰화되어 있다고 생각하자.)
[['나는', '사과를', '좋아해'],
['나는', '바나나를', '좋아해'],
['나는', '사과를', '싫어해'],
['나는', '바나나를', '싫어해']]또한 단어 사전은 다음과 같이 구성되어 있다고 생각해 보자. (간단히 설명하기 위해 스페셜 토큰 등은 제외)
0 '나는'
1 '사과를'
2 '바나나를'
3 '좋아해'
4 '싫어해'자 이제 전체 훈련 데이터를 단어 사전의 index로 변환하면 다음과 같다.
[[0, 1, 3],
[0, 2, 3],
[0, 1, 4],
[0, 2, 4]]위의 matrix가 U가 되는 것이다.
자 이제 U에 대응하는 임베딩 벡터를 찾기 위해 원-핫 인코딩을 수행해 보자.
원-핫 인코딩을 수행한 결과는 다음과 같다.
[[[1,0,0,0,0], [0,1,0,0,0], [0,0,0,1,0]],
[[1,0,0,0,0], [0,0,1,0,0], [0,0,0,1,0]],
[[1,0,0,0,0], [0,1,0,0,0, [0,0,0,0,1]],
[[1,0,0,0,0], [0,0,1,0,0], [0,0,0,0,1]]]위의 3차원 텐서는 (batch_size, seq_len, vocab_size)로 구성되므로 ([4,3,5])가 된다.
따라서 U의 차원은 ([4,3,5])가 되는 것이다.
자 그럼 이제 $W_e$의 차원에 대해 생각해 보자.
$W_e$는 단어 집합의 크기(vocab_size)만큼의 행을 가진 임베딩 행렬이다.
$W_e$는 3차원 텐서로 표현하면 (batch_size, vocab_size, embedding_dim)으로 구성된다.
말 그대로 token embedding matrix 즉, 각 단어(토큰)들의 임베딩 벡터를 가지고 있는 사전이기 때문이다.
따라서 $W_e$의 차원은 ([4,5,768])이 된다. (embedding_dim = 768이라고 가정)
이제 $W_e$와 U를 행렬 곱셈하여, 각 단어에 해당하는 임베딩 벡터를 구한다.
이때 U는 사실상 해당 위치의 단어만 1이고 나머지는 모두 0인 행렬이므로, 이 과정은 $W_e$ matrix에서 해당 단어의 임베딩 벡터만 선택하는 것과 같다. (마치, 단어 사전에서 내가 찾고 싶은 단어의 임베딩 벡터만 가져오는 느낌이다.)
여기서 잠깐 3차원 이상의 텐서(Tensor)의 행렬 곱셈에 대해 짚고 넘어가자.
3차원 이상의 텐서 사이의 행렬 곱셈은 행렬의 차원을 나타내는 마지막 두 개의 차원끼리 행렬 사이에 행렬 곱이 가능하고,
이를 제외한 나머지 차원이 같으면 가능하다. ex) (1,2,3,4,5) x (1,2,3,5,9) = (1,2,3,4,9)
그렇기 때문에 위의 예시에서 U x $W_e$의 차원은 (4,3,5) x (4,5,768) = (4,3,768)이 된다.
즉, ([4,3,768])이라는 것이다.
이제 token embedding matrix $W_p$의 차원에 대해 알아보자.
$W_p$의 차원은 3차원 텐서로 표현했을 때, (batch_size, seq_len, embedding_dim) 으로 구성된다.
즉, ([4,3,768])이다. (어찌 보면 당연하다. $UW_e$랑 더해야 하니까..)
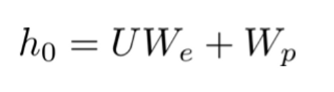
이렇게 구성된 input $h_0$는 Masked self-attention을 수행하기 위한 입력으로 사용된다.
Reference
02-02 텐서 조작하기(Tensor Manipulation) 1
이번 챕터에서 배울 내용에 대해서 리뷰해보겠습니다. 벡터, 행렬, 텐서의 개념에 대해서 이해하고, Numpy와 파이토치로 벡터, 행렬, 텐서를 다루는 방법에 대해서 이해합니…
wikidocs.net
GPT-1 논문 리뷰를 하던 중 문득 "multi-layer transformer decoder를 사용할 때 input으로 사용할 $h_0$는 어떻게 만들어질까?"라는 궁금증이 들었다.

GPT에서 multi-layer transformer decoder를 사용해서 Maksed self-attention을 하기 전에 token들의 context vector(U)와 token embedding matrix($W_e$)를 곱한 후 positional embedding matrix($W_p$)를 더해서 input으로 사용할 $h_0$를 만든다.
이때 각 matrix들의 차원은 어떤 식으로 구성될까?
이를 알기 위해서는 텐서(Tensor)의 개념을 짚고 넘어가야 한다.

딥 러닝을 하게 되면 다루게 되는 가장 기본적인 단위는 벡터, 행렬, 텐서이다. 차원이 없는 값을 스칼라(위의 그림에는 없음), 1차원으로 구성된 값을 벡터라고 한다.
2차원으로 구성된 값을 행렬(Matrix)라고 하고, 3차원이 되면 텐서(Tensor)라고 부른다.
사실 우리는 3차원의 세상에 살고 있으므로, 4차원 이상부터는 머리로 생각하기는 어렵다.
4차원은 3차원의 텐서를 위로 쌓아 올린 모습으로 상상해 보자. 5차원은 그 4차원을 다시 옆으로 확장한 모습이고, 6차원은 5차원을 뒤로 확장한 모습으로 볼 수 있다. (엄밀한 정의는 아니다. 직관적으로 이렇게 이해해보자 라는 것이다.)
Computer Vision 분야에서의 3차원 텐서와 NLP 분야에서의 3차원 텐서는 조금 다르다.
우리는 현재 NLP에서 사용할 것이므로 NLP에서의 3차원 텐서를 살펴보자.
NLP에서는 보통 (batch size, 문장 길이, 단어 벡터의 차원)이라는 3차원 텐서를 사용한다.
직관적으로 표현하면 다음과 같다.

자 이제 3차원 텐서(Tensor)에 대해 이 정도의 개념을 가지고 다시 우리가 알고 싶었던

로 돌아가보자.
쉽게 예제를 통해 이해해보자.
아래와 같이 4개의 문장으로 구성된 전체 훈련 데이터가 있다. (띄어쓰기를 기준으로 토큰화되어 있다고 생각하자.)
[['나는', '사과를', '좋아해'],
['나는', '바나나를', '좋아해'],
['나는', '사과를', '싫어해'],
['나는', '바나나를', '싫어해']]또한 단어 사전은 다음과 같이 구성되어 있다고 생각해 보자. (간단히 설명하기 위해 스페셜 토큰 등은 제외)
0 '나는'
1 '사과를'
2 '바나나를'
3 '좋아해'
4 '싫어해'자 이제 전체 훈련 데이터를 단어 사전의 index로 변환하면 다음과 같다.
[[0, 1, 3],
[0, 2, 3],
[0, 1, 4],
[0, 2, 4]]위의 matrix가 U가 되는 것이다.
자 이제 U에 대응하는 임베딩 벡터를 찾기 위해 원-핫 인코딩을 수행해 보자.
원-핫 인코딩을 수행한 결과는 다음과 같다.
[[[1,0,0,0,0], [0,1,0,0,0], [0,0,0,1,0]],
[[1,0,0,0,0], [0,0,1,0,0], [0,0,0,1,0]],
[[1,0,0,0,0], [0,1,0,0,0, [0,0,0,0,1]],
[[1,0,0,0,0], [0,0,1,0,0], [0,0,0,0,1]]]위의 3차원 텐서는 (batch_size, seq_len, vocab_size)로 구성되므로 ([4,3,5])가 된다.
따라서 U의 차원은 ([4,3,5])가 되는 것이다.
자 그럼 이제 $W_e$의 차원에 대해 생각해 보자.
$W_e$는 단어 집합의 크기(vocab_size)만큼의 행을 가진 임베딩 행렬이다.
$W_e$는 3차원 텐서로 표현하면 (batch_size, vocab_size, embedding_dim)으로 구성된다.
말 그대로 token embedding matrix 즉, 각 단어(토큰)들의 임베딩 벡터를 가지고 있는 사전이기 때문이다.
따라서 $W_e$의 차원은 ([4,5,768])이 된다. (embedding_dim = 768이라고 가정)
이제 $W_e$와 U를 행렬 곱셈하여, 각 단어에 해당하는 임베딩 벡터를 구한다.
이때 U는 사실상 해당 위치의 단어만 1이고 나머지는 모두 0인 행렬이므로, 이 과정은 $W_e$ matrix에서 해당 단어의 임베딩 벡터만 선택하는 것과 같다. (마치, 단어 사전에서 내가 찾고 싶은 단어의 임베딩 벡터만 가져오는 느낌이다.)
여기서 잠깐 3차원 이상의 텐서(Tensor)의 행렬 곱셈에 대해 짚고 넘어가자.
3차원 이상의 텐서 사이의 행렬 곱셈은 행렬의 차원을 나타내는 마지막 두 개의 차원끼리 행렬 사이에 행렬 곱이 가능하고,
이를 제외한 나머지 차원이 같으면 가능하다. ex) (1,2,3,4,5) x (1,2,3,5,9) = (1,2,3,4,9)
그렇기 때문에 위의 예시에서 U x $W_e$의 차원은 (4,3,5) x (4,5,768) = (4,3,768)이 된다.
즉, ([4,3,768])이라는 것이다.
이제 token embedding matrix $W_p$의 차원에 대해 알아보자.
$W_p$의 차원은 3차원 텐서로 표현했을 때, (batch_size, seq_len, embedding_dim) 으로 구성된다.
즉, ([4,3,768])이다. (어찌 보면 당연하다. $UW_e$랑 더해야 하니까..)
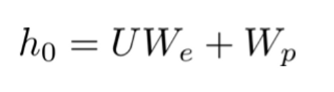
이렇게 구성된 input $h_0$는 Masked self-attention을 수행하기 위한 입력으로 사용된다.
Reference
02-02 텐서 조작하기(Tensor Manipulation) 1
이번 챕터에서 배울 내용에 대해서 리뷰해보겠습니다. 벡터, 행렬, 텐서의 개념에 대해서 이해하고, Numpy와 파이토치로 벡터, 행렬, 텐서를 다루는 방법에 대해서 이해합니…
wikidocs.net
