Conference : ICLR 2023
논문 링크 : https://arxiv.org/pdf/2206.10550.pdf
Abastract
본 논문에서는 off-the-shelf pre-trained model만을 활용해서 $l_2$-norm bounded perturbation에 대한 certified adversarial robustness SOTA를 달성했다.
이를 위해 pretrained DDPM(denoising diffusion probabilistic model)과 high-accuracy classifier를 결합하여 기존의 denoised smoothing approach를 인스턴스화했다.
이러한 방식은 모델의 파라미터를 fine tuning 하거나 retraining 할 필요 없다는 장점을 가진다.
Introduction
bounded propagation 또는 randomized smoothing에 기반한 Certified defense는 norm-bounded adversarial perturbation에서 model의 prediction이 robust 하다는 것을 보장한다.
현재 $l_2$-norm certified robustness SOTA는 randomized smoothing 기법에 의존한다.
input에 대한 random Gaussian perturbation 하에서 “based classifier”가 예측한 label에 대해 다수결 투표를 실시하여 올바른 class가 충분히 자주 출력되면, 원래 노이즈가 없는 input에 대한 defense의 출력은 $l_2$-norm bounded adversarial perturbation에 대해 견고하게 보장된다.
Denoised smoothing은 certified defense의 one-step process를 two-step으로 나눈다. 먼저 randomly perturbed input이 들어오면, “denoiser” model을 통해 noise를 제거한다. 이후 노이즈가 제거된 input을 standard classifier에 적용하는 방식이다.
이러한 방식은 denoiser model이 original training distribution에 가까운 clean 이미지를 생성할 수 있는 한, pretrained standard classfier에 randomized smoothing을 적용할 수 있다.
최근 DDPM에 관련한 연구들(Sohl-Dickstein et al., 2015; Ho et al., 2020; Nichol & Dhariwal, 2021)에서 image generation SOTA를 달성하였고, DDPM의 denoising step이 denoised smoothing의 denoising step과 완벽하게 일치한다. 따라서 Diffusion model을 denoiser model로써 활용할 수 있다.
본 논문에서는 공개적으로 사용가능한 diffusion model과 pretrained SOTA classifier를 결합한다.
Background
Randomized smoothing
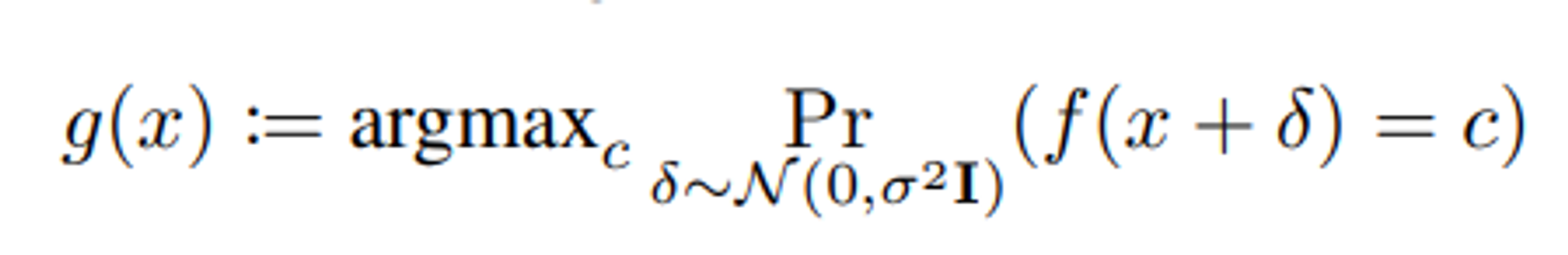
(Cohen et al., 2019)은 smooth classifier g가 l_2 radius R의 perturbation에 대해 robust하다는 것을 증명했다. 여기서 radius R은 classifier의 “margin” (=가장 가능성이 높은 class와 두 번째로 가능성이 높은 class에 할당된 확률의 차이)이 커질수록 증가한다.
- radius $R$의 의미 : Certified robustness에서의 'radius'는 모델이 안정적인 예측을 보증하는 입력 공간의 $L_p$-norm 기준의 크기를 나타낸다. 이 경우, $L_2$-norm이 사용되며, 이는 유클리드 거리(두 점 사이의 직선 거리)에 해당한다.
- 확률 및 radius 계산: 확률은 Clopper-Pearson interval 또는 다른 방법을 사용하여 계산할 수 있으며, 이 확률 값은 통계적으로 낮은 오류율로 클래스의 예측이 변하지 않을 것임을 보증한다. radius는 해당 확률 값에 대한 정규 분포의 역함수(norm.ppf)와 모델에 추가되는 잡음의 정도인 sigma를 곱한 값으로 계산된다.
radius가 크다는 것은 모델이 더 큰 변화에 대해서도 예측을 유지할 것임을 보증한다는 의미이며, 이는 더 강력한 적대적 공격에 대한 내성을 의미한다. 반대로 radius가 작다면 모델이 미묘한 변화에도 불안정할 수 있음을 나타낸다.
여기서 주의해야할 점이 있는데, Certified robustness에서 radius가 크다는 것은 모델이 해당 radius 내의 적대적 변화(perturbation)에 대해 동일한 예측을 할 것임을 보증한다는 뜻이다. 그러나 이는 모델의 예측이 항상 정확하다는 것을 의미하지는 않는다.
즉, 모델이 큰 radius에 대해 'certified'될 수는 있지만, 그것은 모델이 정확한 예측을 하고 있음을 보증하는 것이 아니라 단지 입력에 노이즈가 추가되었을 때 일정한 예측을 유지할 수 있음을 보증하는 것이다
base classifier $f$가 neural network인 경우, Eq.1의 확률을 효율적으로 계산할 수 없기 때문에 (Cohen et al. 2019)은 소수의 noise instance $m$ (eg. $m$=10)을 sampling 하고 입력의 noisy version인 $m$에 대한 base classifier의 출력에 대해 다수결 투표를 수행하여 이 defesne를 인스턴스화한다.
이 defense의 robust radius $R$의 lower-bound를 계산하기 위해 많은 수의 noise instance $\delta$ (eg. $N$=100,000)를 sampling하여 각 class label $c$에 대한 확률 $P[f(x+\delta)=c]$를 추정한다.
Denoised smoothing

(Salman et al., 2020)은 randomized smoothing의 인스턴스화이다.
base classifier $f$는 denoiser와 standard classifier $f_{clf}$로 구성된다.
성능이 좋은 denoiser (즉, $denoise(x+\delta)\approx x$ with hjgh probability for $\delta \sim N(0,\sigma^2I))$)가 주어지면, nosiy image를 input으로 하는 base classifier $f$의 accuracy가 standard classfier $f_{clf}$의 clean accurcay와 유사해짐을 기대할 수 있다.
(Salman et al., 2020)은 Gaussian noise augmentation을 통해 custom denoiser를 training하고, off-the-shelf pretrained classfier와 결합하여 denoised smoothing 기법을 인스턴스화했다.
Diffusion Denoised Smoothing
저자들이 제안하는 Diffusion Denoised Smoothing (DDS)는 이전 섹션에서 소개한 것 이외에 새로운 technical idea가 필요하지 않다.
Denoised smoothing via a diffusion model
이 방법에 필요한 사소한 기술은 randomized smoothing에 필요한 noise model과 diffusion model에서 사용되는 noise model 간의 mapping이다. 구체적으로, randomized smoothing에는 Gaussian noise $x_{rs} \sim N(x, \sigma^2I)$로 보강된 data point가 필요하지만, diffusion model에서는 noise model $x_t \sim N(\sqrt{\alpha_t}x,(1-\alpha_t)I)$를 가정한다.
이때, $x_{rs}$를 $\sqrt{\alpha_t}$로 scaling 하고, 분산을 동일시하면 다음과 같은 관계가 도출된다.
$$ \sigma^2=\frac{1-\alpha_t}{\alpha_t} $$
따라서, 주어진 noise level $\sigma$에서 randomized smoothing을 위해 diffusion model을 사용하려면 먼저
$\sigma^2=\frac{1-\alpha_{t^*}}{\alpha_{t^*}}$ 를 만족하도록 timestep $t^*$를 구해야 한다.
이 방정식의 정확한 공식은 diffusion model에서 사용하는 $\alpha_t$ term의 schedule에 따라 다르지만, 일반적으로 상당히 복잡한 diffusion schedule의 경우에도 closed form으로 계산할 수 있다고 한다.
그럼 다음과 같은 수식을 계산하고,
$$ x_{t^*}=\sqrt{\alpha_{t^*}}(x+\delta), \delta \sim N(0,\sigma^2I) $$
denoised sample의 추정치를 얻기 위해 $x_{t^*}$에 diffusion denoiser를 적용한다.
$$ \widehat{x}=denoise(x_{t^*};t^*) $$
그다음 마지막으로, 추정된 denoised image를 off-the-shelf classifier로 classify 한다.
$$ y=f_{clf}(\widehat{x}) $$
이 과정을 알고리즘으로 정리하면 다음과 같다.

robustness certificate를 얻기 위해, denoising process를 여러 번 반복 (eg., 100,000)하고 Cohen et al., 2019의 approach를 사용하여 certification radius를 계산한다. (diffusion model은 [-1,1]의 입력을 예상하므로 기존 prior work에서 가정한 것처럼 certified radius를 2로 나누어 [0,1]의 입력에 대한 certified radius를 얻는다.)
One-shot denoising
diffusion model에 친숙한 사람들은 $t$시점의 노이즈가 있는 이미지를 $t-1$시점의 약간 적은 노이즈가 있는 이미지로 변환하는 것을 목표로 하는 “single-step” denoising operation $x_{t-1}=d(x_t;t)$를 반복적으로 적용한다는 것을 기억할 수 있다. 이를 full diffusion process로 정의하면 다음과 같다.
$$ \widehat{x}=denoise_{iter}(x+\delta;t):=d(d(...d(d(x+\delta;t);t-1)...;2);1) $$
실제로 one-step denoiser $d$의 각 적용은 two step으로 구성된다.
(1) 현재 time step $t$에서 fully denoised image $x$를 추정하고,
(2) 추정된 denoised image와 이전 timestep $t-1$의 noisy image 사이의 평균을 계산한다. (diffusion model에 따라 적절히 가중치를 부여해서)
따라서 이미지의 노이즈 제거를 위해 전체 t-step diffusion process를 수행하는 대신 diffusion step $d$를 한 번 실행하고, denoised image $x$에 대한 best 추정치를 한 번에 간단히 출력할 수 있다.
diffusion model이 처음부터 image를 생성하려는 경우 (즉, denoiser가 순수한 noise에 적용되는 경우), iterative process는 이러한 one-shot 접근 방식보다 높은 fidelity의 output을 생성한다. (Ho et al., 2020)
그러나 특정 이미지의 노이즈를 제거하려는 경우, one-shot 접근 방식에는 두 가지 장점이 있다.
- High accuacy : standard pretrained classifier는 full $t$-step denoised image에 비해 one-shot denoised image에서 더 정확하다는 것이 밝혀졌다. 저자들은 이를 time step $t$에서 single-step denoiser $d$를 처음 적용할 때, denoiser가 이미 $x$에 대한 모든 정보를 가지고 있기 때문이라고 가정한다. denoiser를 여러 번 적용하면, 각 step마다 새로운(약간 작은) Gaussian noise가 추가되므로 $x$에 대한 정보만 파괴할 수 있기 때문이다. 실제로 iterative $t$-step denoising 전략을 사용하면, 이미지를 채울 방법을 결정하기 위해 classification task의 일부를 denoiser에 떠넘기는 셈이 된다. Section 5에서 이 가설을 실험적으로 검증한다.
- Improved efficiency : 특정 이미지의 noise를 제거하기 위해 수백(또는 수천) 번의 forward pass가 필요한 대신, 오직 단 한번의 pass만 필요하다. 이는 robustness certificate를 얻기 위해 randomized smoothing에 필요한 수천 개의 prediction을 할 때 특히 중요하다.
Evaluation
Dataset : CIFAR-10, ImageNet
Cohen et al., 2019에 따라 CIFAR-10에서는 $N$=100,000, ImageNet에서는 $N$=10,000 sample만을 사용한다.
이전 work들의 setting에 따라 $\sigma \in\left\{0.25,0.5,1.0\right\}$를 사용한다.
Table 1과 Table 2에서 이전 work들과의 pair comparison을 위해 3개의 $\sigma$중 가장 best result를 report했다.
또한 기존 work들은 computational overhead 때문에 3가지 noise level을 사용했지만, diffusion model의 한 가지 이점은 새로운 denoiser model을 학습시키지 않고도 다른 양의 noise($\sigma$)를 사용할 수 있다는 것이다.
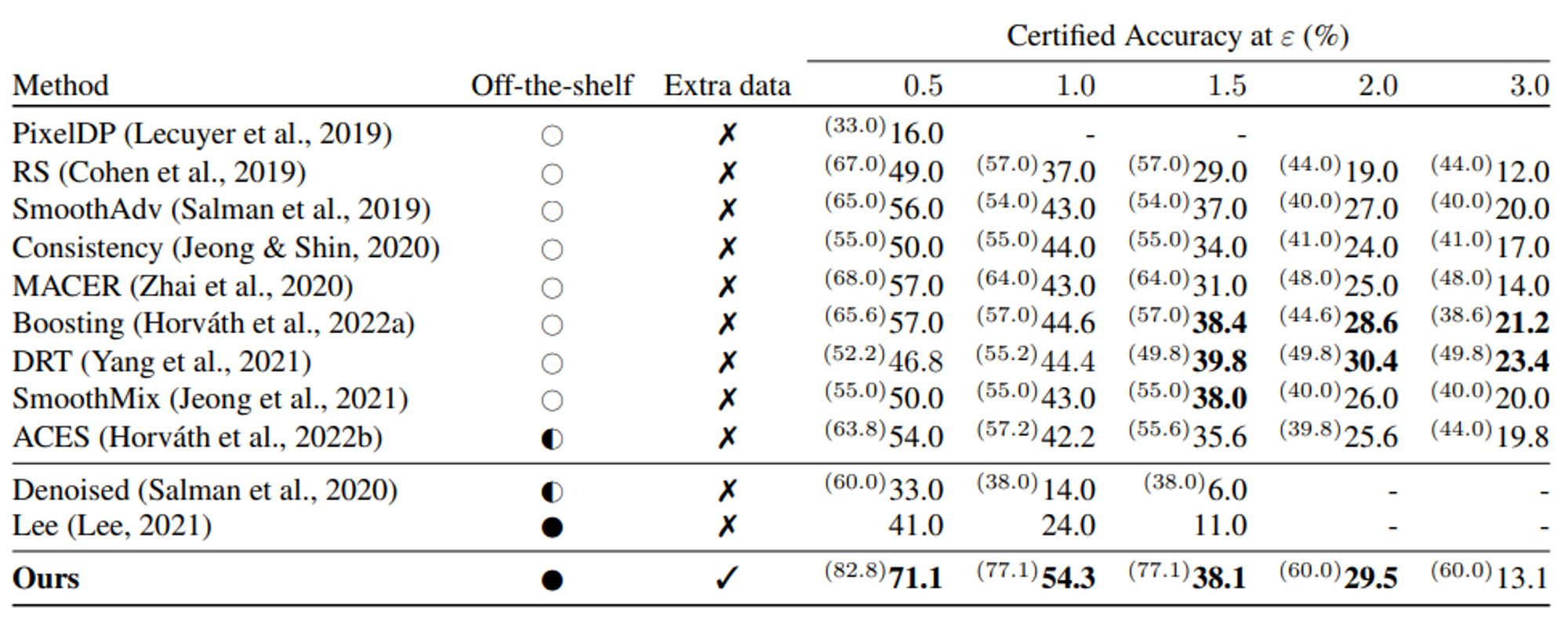
- ImageNet configuration
- diffusion model : 552M-parameter classunconditional diffusion model from Dhariwal & Nichol (2021)
- classifier : 305M parameter BEiT large model (Bao et al., 2022) which reaches a 88.6% top-1 validation accuracy using the implementation from timm (Wightman, 2019).
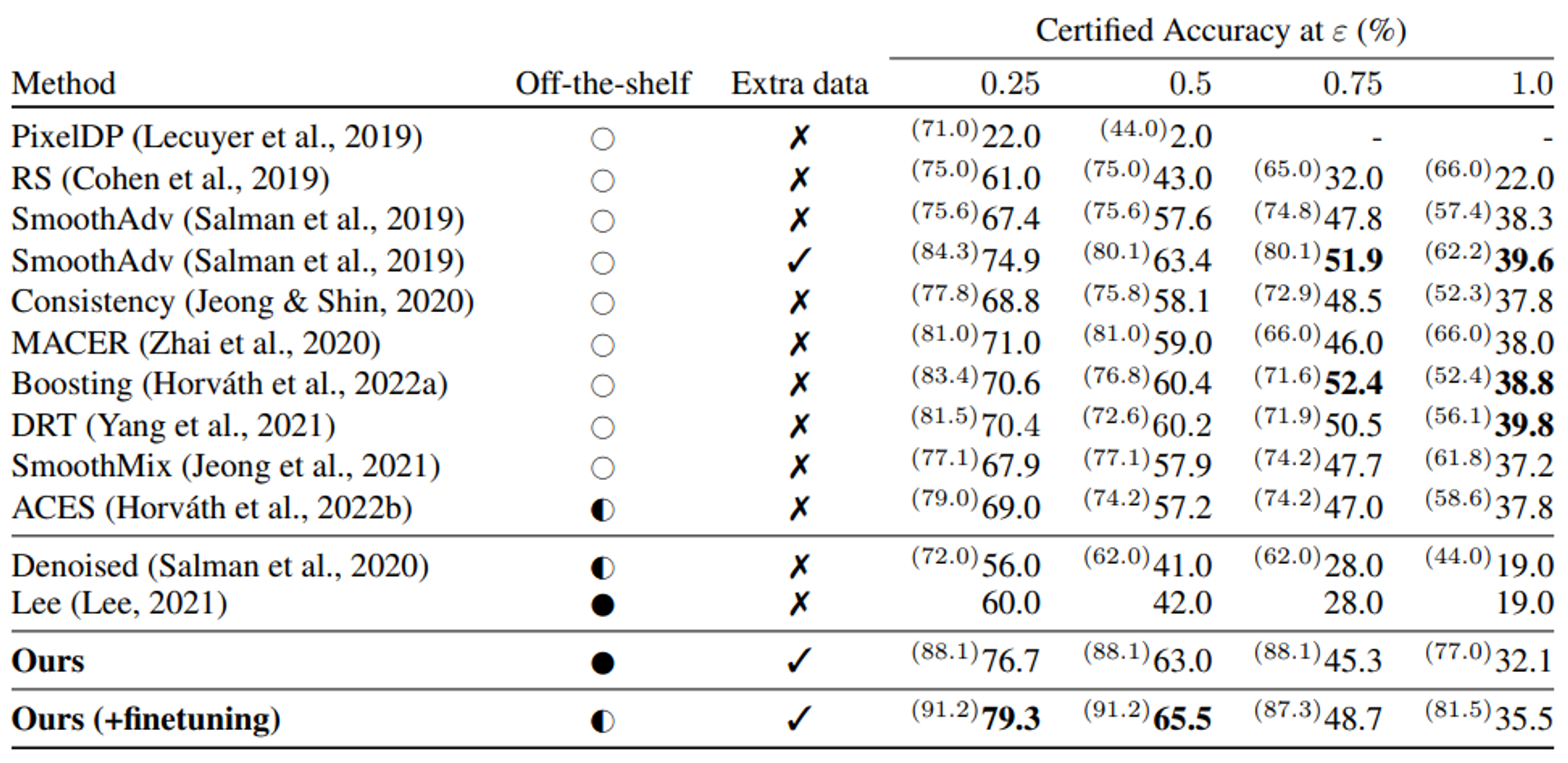
- CIFAR-10 configuration
- diffusion model : 50M-parameter diffusion model from Nichol & Dhariwal (2021)
- classifier : 87M-parameter ViT-B/16 model (Dosovitskiy et al., 2021) that was pretrained on ImageNet-21k (Deng et al., 2009) (in 224 × 224 resolution) and finetuned on CIFAR-10.
Analysis and Discussion
저자들은 diffusion model을 trivial denoiser로써 사용함에도 불구하고 SOTA certified accuracy를 달성했다.
즉, diffusion model이 다양한 noise level에 걸쳐 이미지를 반복적으로 개선할 수 있다는 사실을 활용하는 대신, 고정된 noise level에 대해 diffusion model을 한 번만 적용하여 one-shot denoising을 수행한다.
본 섹션에서는 이러한 접근법이 denoised smoothing을 위해 denoiser를 학습시킨 이전 work (Salman et al., 2020)보다 성능이 우수한 이유와 one-shot denoising에 diffusion model을 사용하는 것이 복잡한 iterative diffusion process보다 성능이 우수한 이유에 대해 알아본다.
Full Diffusion versus One-shot Denoising
Diffusion이 generative model로 사용되는 경우, timestep $t$에 해당하는 크기의 noise가 있는 이미지 $x_t$가 주어지면, 모델은 먼저 denoised 이미지 $x_0$에 대한 one-shot 추정치를 예측한 다음, 적절한 가중치를 사용하여 $x_0, x_t$와 새로운 isotropic Gaussian noise $N(0,I)$를 interpolating 해서 timestep $t-1$의 이미지를 estimate 한다.
그다음 diffusion process가 timestep $t-1$에서 recursive 하게 적용된다.
저자들은 직관적으로 diffusion model을 denoiser로써 사용할 때, one-shot denoising이 full iterative reverse-diffusion process보다 더 faithful 한 결과를 생성할 것으로 예상할 수 있다고 주장한다.
실제로 reverse-diffusion process의 각 step은 이미지에 새로운 Gaussian noise를 추가하기 때문에 원본 이미지에 대한 정보를 파괴한다. 따라서 적어도 이론적으로는 여러 번 반복하는 것보다 한 번에 denoising 하는 것이 더 쉬울 것이라고 한다.
full reverse-diffusion process는 더 세밀한 디테일이 있는 노이즈 제거 이미지를 생성하지만, 이러한 디테일은 실제로 denoising을 하려는 원본 이미지에 faithful 하지 않은 경우가 많고, 눈에 띄는 디테일을 “hallucinate”하는 경향이 있다는 것을 아래의 Figure를 통해 보여준다.

one-shot denosing은 원본 이미지의 대부분을 faithful 하고 흐릿하게 재구성하는 반면, full reverse-diffusion process는 새로운 디테일을 “발명”해서 궁극적으로 더 사실적이지만 원본 이미지와는 의미적으로 다른 이미지를 생성하는 것을 볼 수 있다.
Conference : ICLR 2023
논문 링크 : https://arxiv.org/pdf/2206.10550.pdf
Abastract
본 논문에서는 off-the-shelf pre-trained model만을 활용해서 $l_2$-norm bounded perturbation에 대한 certified adversarial robustness SOTA를 달성했다.
이를 위해 pretrained DDPM(denoising diffusion probabilistic model)과 high-accuracy classifier를 결합하여 기존의 denoised smoothing approach를 인스턴스화했다.
이러한 방식은 모델의 파라미터를 fine tuning 하거나 retraining 할 필요 없다는 장점을 가진다.
Introduction
bounded propagation 또는 randomized smoothing에 기반한 Certified defense는 norm-bounded adversarial perturbation에서 model의 prediction이 robust 하다는 것을 보장한다.
현재 $l_2$-norm certified robustness SOTA는 randomized smoothing 기법에 의존한다.
input에 대한 random Gaussian perturbation 하에서 “based classifier”가 예측한 label에 대해 다수결 투표를 실시하여 올바른 class가 충분히 자주 출력되면, 원래 노이즈가 없는 input에 대한 defense의 출력은 $l_2$-norm bounded adversarial perturbation에 대해 견고하게 보장된다.
Denoised smoothing은 certified defense의 one-step process를 two-step으로 나눈다. 먼저 randomly perturbed input이 들어오면, “denoiser” model을 통해 noise를 제거한다. 이후 노이즈가 제거된 input을 standard classifier에 적용하는 방식이다.
이러한 방식은 denoiser model이 original training distribution에 가까운 clean 이미지를 생성할 수 있는 한, pretrained standard classfier에 randomized smoothing을 적용할 수 있다.
최근 DDPM에 관련한 연구들(Sohl-Dickstein et al., 2015; Ho et al., 2020; Nichol & Dhariwal, 2021)에서 image generation SOTA를 달성하였고, DDPM의 denoising step이 denoised smoothing의 denoising step과 완벽하게 일치한다. 따라서 Diffusion model을 denoiser model로써 활용할 수 있다.
본 논문에서는 공개적으로 사용가능한 diffusion model과 pretrained SOTA classifier를 결합한다.
Background
Randomized smoothing
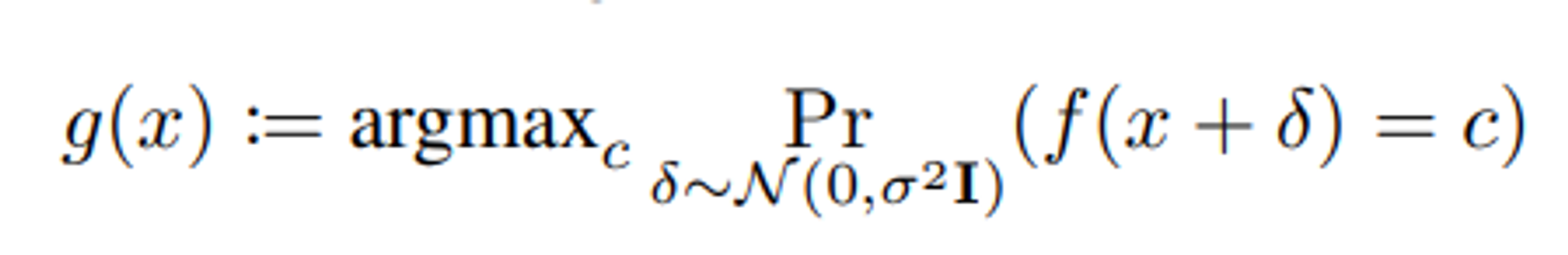
(Cohen et al., 2019)은 smooth classifier g가 l_2 radius R의 perturbation에 대해 robust하다는 것을 증명했다. 여기서 radius R은 classifier의 “margin” (=가장 가능성이 높은 class와 두 번째로 가능성이 높은 class에 할당된 확률의 차이)이 커질수록 증가한다.
- radius $R$의 의미 : Certified robustness에서의 'radius'는 모델이 안정적인 예측을 보증하는 입력 공간의 $L_p$-norm 기준의 크기를 나타낸다. 이 경우, $L_2$-norm이 사용되며, 이는 유클리드 거리(두 점 사이의 직선 거리)에 해당한다.
- 확률 및 radius 계산: 확률은 Clopper-Pearson interval 또는 다른 방법을 사용하여 계산할 수 있으며, 이 확률 값은 통계적으로 낮은 오류율로 클래스의 예측이 변하지 않을 것임을 보증한다. radius는 해당 확률 값에 대한 정규 분포의 역함수(norm.ppf)와 모델에 추가되는 잡음의 정도인 sigma를 곱한 값으로 계산된다.
radius가 크다는 것은 모델이 더 큰 변화에 대해서도 예측을 유지할 것임을 보증한다는 의미이며, 이는 더 강력한 적대적 공격에 대한 내성을 의미한다. 반대로 radius가 작다면 모델이 미묘한 변화에도 불안정할 수 있음을 나타낸다.
여기서 주의해야할 점이 있는데, Certified robustness에서 radius가 크다는 것은 모델이 해당 radius 내의 적대적 변화(perturbation)에 대해 동일한 예측을 할 것임을 보증한다는 뜻이다. 그러나 이는 모델의 예측이 항상 정확하다는 것을 의미하지는 않는다.
즉, 모델이 큰 radius에 대해 'certified'될 수는 있지만, 그것은 모델이 정확한 예측을 하고 있음을 보증하는 것이 아니라 단지 입력에 노이즈가 추가되었을 때 일정한 예측을 유지할 수 있음을 보증하는 것이다
base classifier $f$가 neural network인 경우, Eq.1의 확률을 효율적으로 계산할 수 없기 때문에 (Cohen et al. 2019)은 소수의 noise instance $m$ (eg. $m$=10)을 sampling 하고 입력의 noisy version인 $m$에 대한 base classifier의 출력에 대해 다수결 투표를 수행하여 이 defesne를 인스턴스화한다.
이 defense의 robust radius $R$의 lower-bound를 계산하기 위해 많은 수의 noise instance $\delta$ (eg. $N$=100,000)를 sampling하여 각 class label $c$에 대한 확률 $P[f(x+\delta)=c]$를 추정한다.
Denoised smoothing

(Salman et al., 2020)은 randomized smoothing의 인스턴스화이다.
base classifier $f$는 denoiser와 standard classifier $f_{clf}$로 구성된다.
성능이 좋은 denoiser (즉, $denoise(x+\delta)\approx x$ with hjgh probability for $\delta \sim N(0,\sigma^2I))$)가 주어지면, nosiy image를 input으로 하는 base classifier $f$의 accuracy가 standard classfier $f_{clf}$의 clean accurcay와 유사해짐을 기대할 수 있다.
(Salman et al., 2020)은 Gaussian noise augmentation을 통해 custom denoiser를 training하고, off-the-shelf pretrained classfier와 결합하여 denoised smoothing 기법을 인스턴스화했다.
Diffusion Denoised Smoothing
저자들이 제안하는 Diffusion Denoised Smoothing (DDS)는 이전 섹션에서 소개한 것 이외에 새로운 technical idea가 필요하지 않다.
Denoised smoothing via a diffusion model
이 방법에 필요한 사소한 기술은 randomized smoothing에 필요한 noise model과 diffusion model에서 사용되는 noise model 간의 mapping이다. 구체적으로, randomized smoothing에는 Gaussian noise $x_{rs} \sim N(x, \sigma^2I)$로 보강된 data point가 필요하지만, diffusion model에서는 noise model $x_t \sim N(\sqrt{\alpha_t}x,(1-\alpha_t)I)$를 가정한다.
이때, $x_{rs}$를 $\sqrt{\alpha_t}$로 scaling 하고, 분산을 동일시하면 다음과 같은 관계가 도출된다.
$$ \sigma^2=\frac{1-\alpha_t}{\alpha_t} $$
따라서, 주어진 noise level $\sigma$에서 randomized smoothing을 위해 diffusion model을 사용하려면 먼저
$\sigma^2=\frac{1-\alpha_{t^*}}{\alpha_{t^*}}$ 를 만족하도록 timestep $t^*$를 구해야 한다.
이 방정식의 정확한 공식은 diffusion model에서 사용하는 $\alpha_t$ term의 schedule에 따라 다르지만, 일반적으로 상당히 복잡한 diffusion schedule의 경우에도 closed form으로 계산할 수 있다고 한다.
그럼 다음과 같은 수식을 계산하고,
$$ x_{t^*}=\sqrt{\alpha_{t^*}}(x+\delta), \delta \sim N(0,\sigma^2I) $$
denoised sample의 추정치를 얻기 위해 $x_{t^*}$에 diffusion denoiser를 적용한다.
$$ \widehat{x}=denoise(x_{t^*};t^*) $$
그다음 마지막으로, 추정된 denoised image를 off-the-shelf classifier로 classify 한다.
$$ y=f_{clf}(\widehat{x}) $$
이 과정을 알고리즘으로 정리하면 다음과 같다.

robustness certificate를 얻기 위해, denoising process를 여러 번 반복 (eg., 100,000)하고 Cohen et al., 2019의 approach를 사용하여 certification radius를 계산한다. (diffusion model은 [-1,1]의 입력을 예상하므로 기존 prior work에서 가정한 것처럼 certified radius를 2로 나누어 [0,1]의 입력에 대한 certified radius를 얻는다.)
One-shot denoising
diffusion model에 친숙한 사람들은 $t$시점의 노이즈가 있는 이미지를 $t-1$시점의 약간 적은 노이즈가 있는 이미지로 변환하는 것을 목표로 하는 “single-step” denoising operation $x_{t-1}=d(x_t;t)$를 반복적으로 적용한다는 것을 기억할 수 있다. 이를 full diffusion process로 정의하면 다음과 같다.
$$ \widehat{x}=denoise_{iter}(x+\delta;t):=d(d(...d(d(x+\delta;t);t-1)...;2);1) $$
실제로 one-step denoiser $d$의 각 적용은 two step으로 구성된다.
(1) 현재 time step $t$에서 fully denoised image $x$를 추정하고,
(2) 추정된 denoised image와 이전 timestep $t-1$의 noisy image 사이의 평균을 계산한다. (diffusion model에 따라 적절히 가중치를 부여해서)
따라서 이미지의 노이즈 제거를 위해 전체 t-step diffusion process를 수행하는 대신 diffusion step $d$를 한 번 실행하고, denoised image $x$에 대한 best 추정치를 한 번에 간단히 출력할 수 있다.
diffusion model이 처음부터 image를 생성하려는 경우 (즉, denoiser가 순수한 noise에 적용되는 경우), iterative process는 이러한 one-shot 접근 방식보다 높은 fidelity의 output을 생성한다. (Ho et al., 2020)
그러나 특정 이미지의 노이즈를 제거하려는 경우, one-shot 접근 방식에는 두 가지 장점이 있다.
- High accuacy : standard pretrained classifier는 full $t$-step denoised image에 비해 one-shot denoised image에서 더 정확하다는 것이 밝혀졌다. 저자들은 이를 time step $t$에서 single-step denoiser $d$를 처음 적용할 때, denoiser가 이미 $x$에 대한 모든 정보를 가지고 있기 때문이라고 가정한다. denoiser를 여러 번 적용하면, 각 step마다 새로운(약간 작은) Gaussian noise가 추가되므로 $x$에 대한 정보만 파괴할 수 있기 때문이다. 실제로 iterative $t$-step denoising 전략을 사용하면, 이미지를 채울 방법을 결정하기 위해 classification task의 일부를 denoiser에 떠넘기는 셈이 된다. Section 5에서 이 가설을 실험적으로 검증한다.
- Improved efficiency : 특정 이미지의 noise를 제거하기 위해 수백(또는 수천) 번의 forward pass가 필요한 대신, 오직 단 한번의 pass만 필요하다. 이는 robustness certificate를 얻기 위해 randomized smoothing에 필요한 수천 개의 prediction을 할 때 특히 중요하다.
Evaluation
Dataset : CIFAR-10, ImageNet
Cohen et al., 2019에 따라 CIFAR-10에서는 $N$=100,000, ImageNet에서는 $N$=10,000 sample만을 사용한다.
이전 work들의 setting에 따라 $\sigma \in\left\{0.25,0.5,1.0\right\}$를 사용한다.
Table 1과 Table 2에서 이전 work들과의 pair comparison을 위해 3개의 $\sigma$중 가장 best result를 report했다.
또한 기존 work들은 computational overhead 때문에 3가지 noise level을 사용했지만, diffusion model의 한 가지 이점은 새로운 denoiser model을 학습시키지 않고도 다른 양의 noise($\sigma$)를 사용할 수 있다는 것이다.

- ImageNet configuration
- diffusion model : 552M-parameter classunconditional diffusion model from Dhariwal & Nichol (2021)
- classifier : 305M parameter BEiT large model (Bao et al., 2022) which reaches a 88.6% top-1 validation accuracy using the implementation from timm (Wightman, 2019).

- CIFAR-10 configuration
- diffusion model : 50M-parameter diffusion model from Nichol & Dhariwal (2021)
- classifier : 87M-parameter ViT-B/16 model (Dosovitskiy et al., 2021) that was pretrained on ImageNet-21k (Deng et al., 2009) (in 224 × 224 resolution) and finetuned on CIFAR-10.
Analysis and Discussion
저자들은 diffusion model을 trivial denoiser로써 사용함에도 불구하고 SOTA certified accuracy를 달성했다.
즉, diffusion model이 다양한 noise level에 걸쳐 이미지를 반복적으로 개선할 수 있다는 사실을 활용하는 대신, 고정된 noise level에 대해 diffusion model을 한 번만 적용하여 one-shot denoising을 수행한다.
본 섹션에서는 이러한 접근법이 denoised smoothing을 위해 denoiser를 학습시킨 이전 work (Salman et al., 2020)보다 성능이 우수한 이유와 one-shot denoising에 diffusion model을 사용하는 것이 복잡한 iterative diffusion process보다 성능이 우수한 이유에 대해 알아본다.
Full Diffusion versus One-shot Denoising
Diffusion이 generative model로 사용되는 경우, timestep $t$에 해당하는 크기의 noise가 있는 이미지 $x_t$가 주어지면, 모델은 먼저 denoised 이미지 $x_0$에 대한 one-shot 추정치를 예측한 다음, 적절한 가중치를 사용하여 $x_0, x_t$와 새로운 isotropic Gaussian noise $N(0,I)$를 interpolating 해서 timestep $t-1$의 이미지를 estimate 한다.
그다음 diffusion process가 timestep $t-1$에서 recursive 하게 적용된다.
저자들은 직관적으로 diffusion model을 denoiser로써 사용할 때, one-shot denoising이 full iterative reverse-diffusion process보다 더 faithful 한 결과를 생성할 것으로 예상할 수 있다고 주장한다.
실제로 reverse-diffusion process의 각 step은 이미지에 새로운 Gaussian noise를 추가하기 때문에 원본 이미지에 대한 정보를 파괴한다. 따라서 적어도 이론적으로는 여러 번 반복하는 것보다 한 번에 denoising 하는 것이 더 쉬울 것이라고 한다.
full reverse-diffusion process는 더 세밀한 디테일이 있는 노이즈 제거 이미지를 생성하지만, 이러한 디테일은 실제로 denoising을 하려는 원본 이미지에 faithful 하지 않은 경우가 많고, 눈에 띄는 디테일을 “hallucinate”하는 경향이 있다는 것을 아래의 Figure를 통해 보여준다.

one-shot denosing은 원본 이미지의 대부분을 faithful 하고 흐릿하게 재구성하는 반면, full reverse-diffusion process는 새로운 디테일을 “발명”해서 궁극적으로 더 사실적이지만 원본 이미지와는 의미적으로 다른 이미지를 생성하는 것을 볼 수 있다.
